Finite volume method for computational fluid dynamics (CFD)
Finite Volume Method for Computational Fluid Dynamics (CFD)

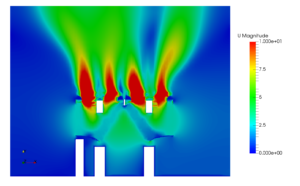
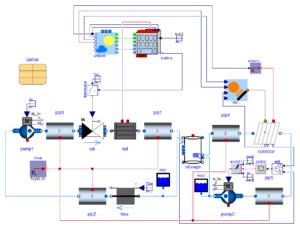
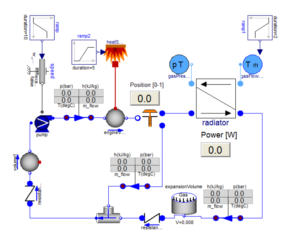
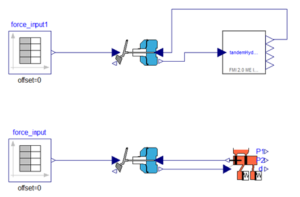
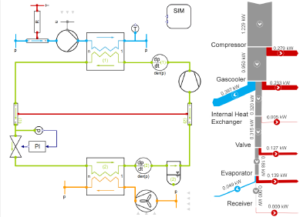
Finite volume method (FVM) is a technique, that is used to solve the governing partial differential equations (PDEs) for fluid flow and heat transfer. While the actual governing PDEs can’t be solved analytically for complex domain, FVM solves them by converting to algebraic equations. In this method the equations are solved at finite number of discrete points in a geometry. Most of the computational fluid & heat transfer solvers are based on FVM technique.
Advantages Of Finite Volume Method:
The main advantage of using this method in comparison to Finite Difference Method (FDM), that it can be used with unstructured grids. This helps in capturing complex geometry. That is exactly why this method is employed in most of the commercial and open source CFD packages. Moreover, the FVM approach ensures the conservation of mass, momentum and energy. Since the finite volume method used integral formulations of conservation laws in case of discontinuities the assumption of smoothness does not come into picture. In scenarios such as compressible flows where shocks might be present, FVM approach might be preferable over the other discretization methods.
The spatial discretization is carried out in the physical space in the finite volume method, thus resulting in less transformations between co-ordinate systems, unlike Finite Element Analysis (FEA). The most attractive feature of this method is that it can compute weak solutions of the governing equations in a very straight forward manner.




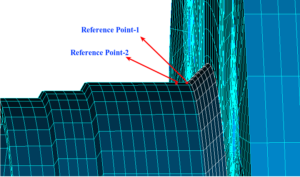
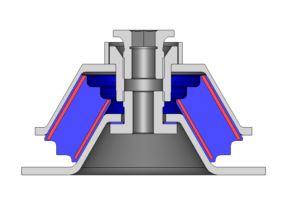
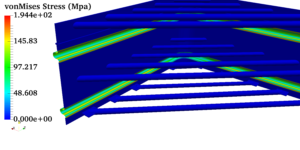
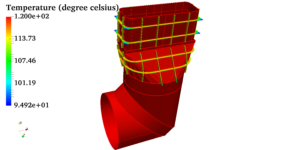
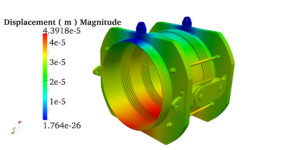
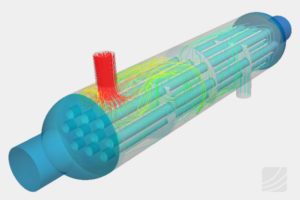
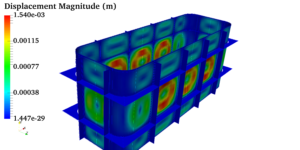 Pressure vessels, pipes, expansion joints etc. are basic equipments for process industries. Pressure vessels are vessels working under internal, external or vacuum pressure, and possibly subjected to high temperature. Proper design and analysis is very important for the pressure vessels, as their failure can cause lot of hazards. Codes/ standards are used in the design phase, followed by analysis to ascertain stresses are within the allowable range. ASME provides wide range of guidelines for the proper design of such vessels.
Pressure vessels, pipes, expansion joints etc. are basic equipments for process industries. Pressure vessels are vessels working under internal, external or vacuum pressure, and possibly subjected to high temperature. Proper design and analysis is very important for the pressure vessels, as their failure can cause lot of hazards. Codes/ standards are used in the design phase, followed by analysis to ascertain stresses are within the allowable range. ASME provides wide range of guidelines for the proper design of such vessels.