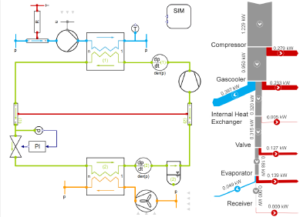
Use of Relaxation Factors in CFD Analysis
Use of Relaxation Factors in CFD Analysis
Field and Equation Under-relaxations:
Under-relaxation is a fraction, often used in iterative methods to stabilize the linear solvers. Let’s assume a transport equation is solved for variable ϕ. As iterative method is being followed, the value of ϕ can get updated in subsequent iterations. At beginning of present iteration let’s denote the transport variable as ϕpi and after the iteration the variable value as ϕai. The difference (ϕai − ϕpi) can be under-relaxed by a factor α and added back to ϕpi for the next iteration. Hence for the next iteration the value of ϕ would be ϕpi + α(ϕai − ϕpi). This kind of under-relaxation is applied after evaluating the value of ϕ after each iteration and is known as field under-relaxation. As it requires to store a new variable this kind of under-relaxation require more computational resource.
However, instead of storing an additional variable, the concept of under-relaxation can be explicitly included in transport equations, then this is known as equation under-relaxation.
Diagonal Dominance of Matrix and Under-relaxation:
The iterative methods have specific known sufficient criteria for convergence. For example, the sufficient criteria for convergence for Gauss Seidel is a diagonal-dominated matrix (weak diagonal dominance). Normally transport equations for fluid flow satisfy weak-diagonal dominant condition. However, it is not always guaranteed to have a diagonal dominant matrix due to advection terms present in transport equations. A weak diagonal dominant matrix has diagonal terms larger or equal in magnitude than sum of magnitude of other entries in a row. To read in more details about diagonal dominance section 5.5 of the book by Greenshields and Weller “Notes on Computational Fluid Dynamics: General Principles” can be referred. Dividing the diagonal terms with fractions can help making the magnitude of diagonal terms larger. This is how the under-relaxations can help.
Pressure velocity coupling algorithms and under-relaxation:
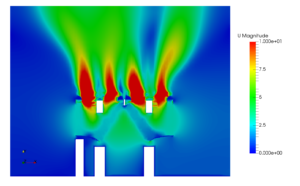
The requirement of under-relaxation is also linked to the pressure and velocity coupling algorithm chosen to solve a transport equation. SIMPLE algorithm is based on an assumed pressure field. Also, during the algorithmic steps, it ignores specific terms, which introduces an error in the iteration. Therefore, an under-relaxation factor is required for pressure and velocity fields. In contrast, SIMPLEC algorithm does not have this limitation, hence an under-relaxation for pressure is not required. However, an under-relaxation in velocity and other scalars are provided in both SIMPLE and SIMPLEC. The PISO algorithm, being used for transient simulations, does not require any under-relaxation as the transient equations with Co < 1, would be diagonally dominant due to higher magnitude of diagonal term (related to time derivatives) over the advection terms.
Value ranges of under-relaxation:
The lower the under-relaxation, more stable is the solution. However, a value around 0.2 is highly restrictive for the solution to march. Such a lower relaxation indicates a problem in combination of schemes and boundary conditions. Hence, suitable change should be made in the CFD solver settings. A higher relaxation ( ≥ 0.7) is always desirable. Also, apart from stability of solver, the residual plots should be monitored and the relaxation should be altered to achieve a lower order residual.
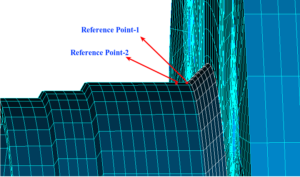
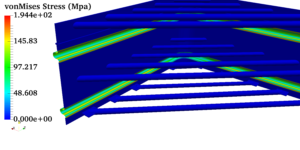
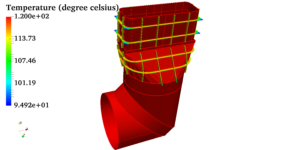
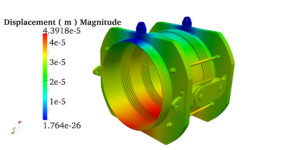
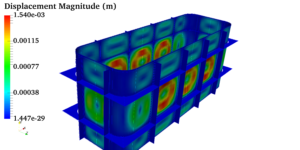Pressure vessels, pipes, expansion joints etc. are basic equipments for process industries. Pressure vessels are vessels working under internal, external or vacuum pressure, and possibly subjected to high temperature. Proper design and analysis is very important for the pressure vessels, as their failure can cause lot of hazards. Codes/ standards are used in the design phase, followed by analysis to ascertain stresses are within the allowable range. ASME provides wide range of guidelines for the proper design of such vessels.
